Models cascade
System overview
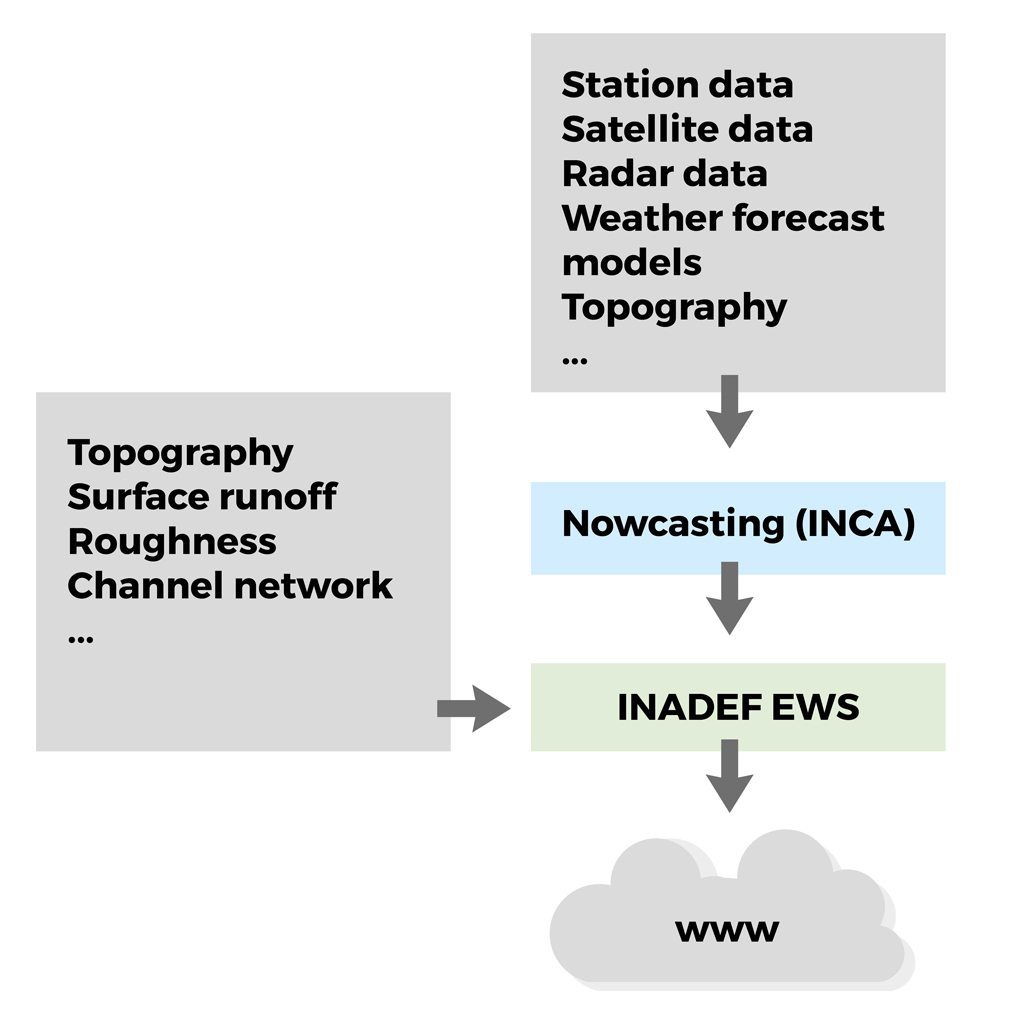
The overall view of the system includes the following components:
- Local agencies providing corrected radar data;
- The INCA model by ZAMG, that uses the radar data along with other inputs to generate rainfall nowcasting maps;
- The INADEF-EWS (Early Warning System), that uses the nowcasting maps along with other input data to generate early warning maps and alerts.
INADEF-EWS
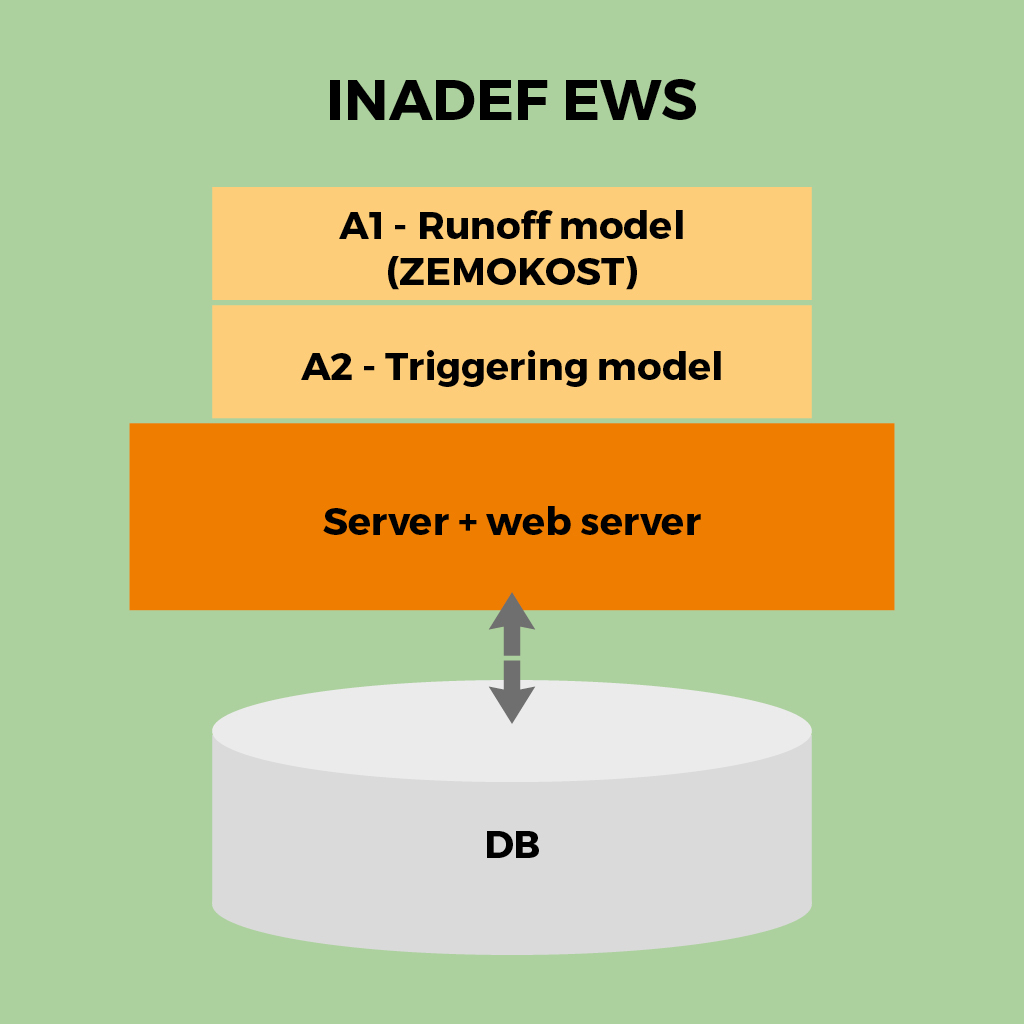
The INADEF-EWS system is in turn made of several subsystems:
- A server in charge of:
- Receiving and storing the nowcasting data from ZAMG;
- Running the ZEMOKOST runoff model by BFW;
- Running the triggering model by UNIPD;
- A DBMS (Database Management System) with spatial extension to store input and output data for and from the models;
- A web server to disseminate the simulation results (maps, tables, reports…).
Data flows
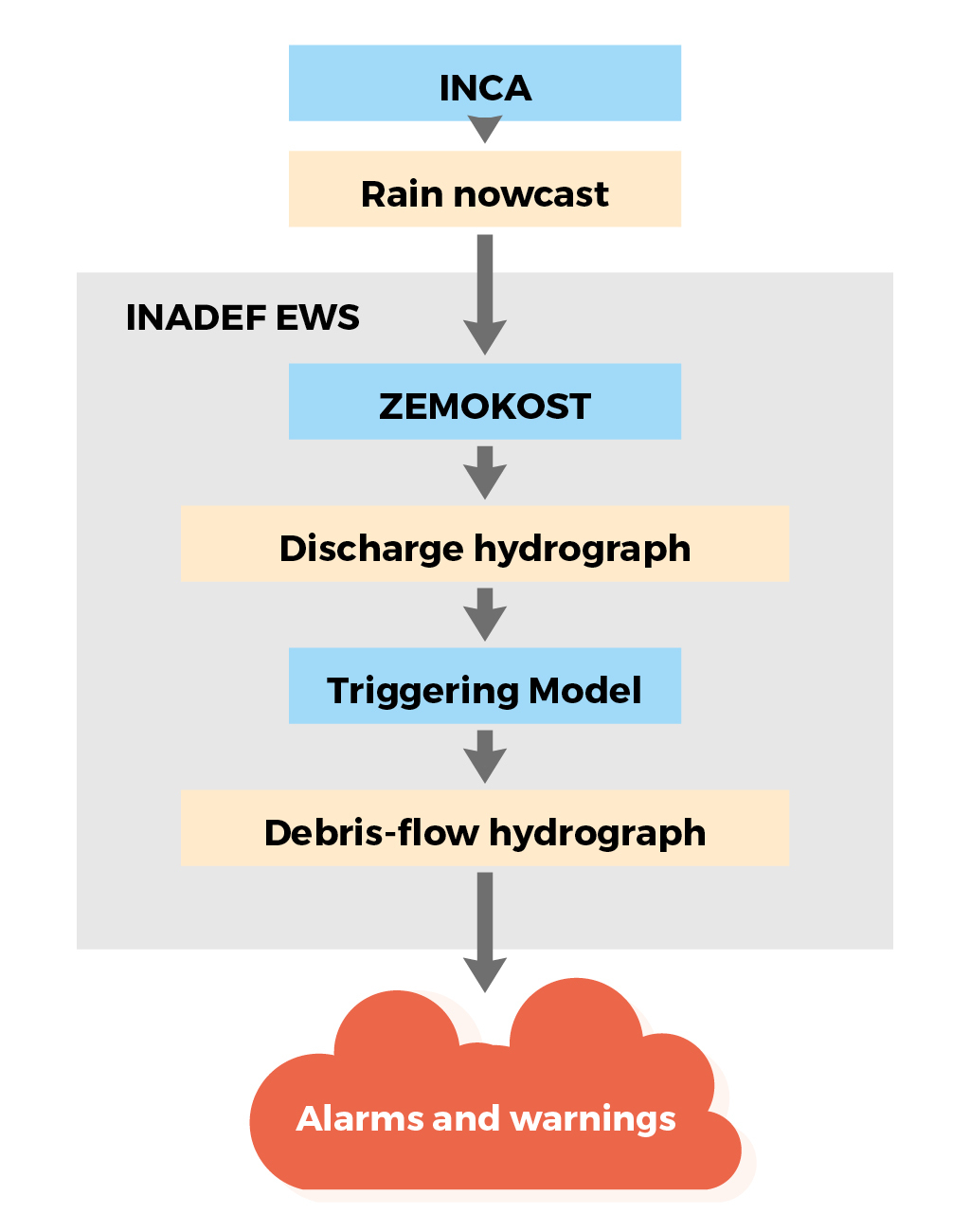
- Local agencies (ARPAV, ZAMG) provide radar data to be fed into the INCA nowcasting model;
- INCA produces rainfall nowcasting maps, that are delivered to the INADEF-EWS;
- INADEF-EWS feeds the nowcasting data, along with all other inputs needed, to ZEMOKOST;
- INADEF-EWS feeds the outputs from the ZEMOKOST model to the debris flow triggering model;
INADEF-EWS processes the outputs from the triggering model and disseminates useful information (alarms, warnings) via the web.
INCA - ZAMG
INCA is a multi-parameter analysis and nowcasting system that has been developed at the Austrian Met Service ZAMG. It is making use of various input data such as ground observations, radar, satellite data and NWP background information in order to produce gridded analysis and nowcasting fields of precipitation, precipitation type, temperature, humidity, wind, cloudiness, snowfall line and many other meteorological quantities.
INCA nowcast fields are extrapolation-based and may be blended into NWP forecasts, thus providing a seamless chain of forecast products from time zero up to a few days ahead. INCA output may also be used as input for applications in other fields, such as in hydrological runoff modelling or debris flow modelling.


INCA is very fast, i.e. it is able to produce output fields within a few minutes after the observations have been received. Therefore INCA provides useful information at a very early stage when NWP information is not yet available. However, as INCA is an observation based system, the quality of the resulting products is heavily depending on the timely availability and quality of the input data.
- Domain: 8.5°-17.7° E and 45.8°– 49.4° N, covering Austria and parts of the neighbouring countries (i.e. parts of northern Italy)
- Resolution is 1 x 1 km (701 x 401 grid points)
- Update frequency and forecast time step: 5min or 15min for precipitation, 1h for temperature, humidity, wind, etc.
- Nowcast range: 1-4 hours for precipitation and 6-12 hours for other parameters
- After nowcasting range, the fields are blended into NWP forecasts with a forecast range of up to 48 hours
ZEMOKOST-BFW
Zemokost is a conceptual precipitation-runoff model for ungauged torrent catchments. The two most important input parameters are:
- Spatial description of the catchment area
- Precipitation
Spatial description: the channel network, described by flow length, gradient and flow roughness, is divided by nodes. For each node a hydrological catchment area is needed (sub-catchment). For each sub- catchment information about the roughness and runoff coefficient as well as terrain specifications (area, inclination, etc.) is required.
In this model chain the precipitation is obtained from the INCA data. INCA offers quarter-hourly precipitation data with a resolution of 1*1 km. The minute values required for ZEMOKOST are obtained by interpolation. The precipitation is determined by the intersection of the precipitation pixels with the (sub) catchment areas, the weighting is based on the area proportion of each pixel in the catchment area.
The runoff of each sub-catchment area is summarized in the corresponding node and forwarded to the sub-catchment area below until the last node in the spatial description is reached. After the modeling, the discharges are available, in m³/s every minute, for each node and each sub-catchment area.
TRIGGERING MODEL
- Runoff volume contributing to debris flow
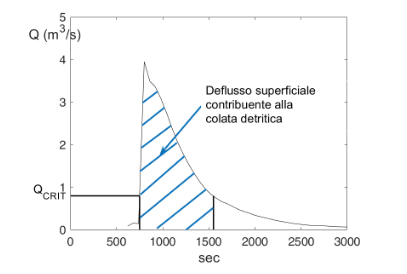
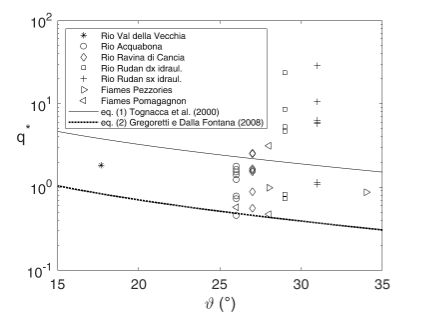
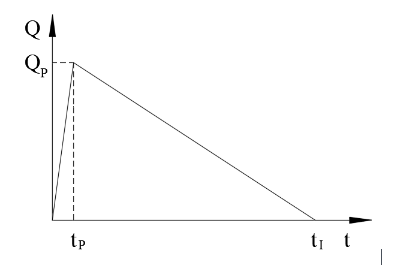
The runoff contributing volume to debris flow is that corresponding to the part of runoff hydrograph exceeding the critical discharge for the debris-flow generation (figure 1). Such a concept was initially introduced by Bennet et al. (2014), and later resumed by Gregoretti et al. (2016b). The critical discharge is the liquid discharge able to entrain the large quantity of sediments needed for the formation of a solid-liquid current (figure 2) and was firstly estimated by Tognacca et al. (2000) through an empirical relationship based on laboratory-flume experiments of debris-flow generation:
qCRIT =4dM1.5 tanϑ-1.17 (1)
where qCRIT is the unit width critical discharge, dM the mean diameter of sediments and ϑ the bed slope angle. Gregoretti and Dalla Fontana (2008) proposed an analogous relationship based on laboratory flume experiments of the inception of high rate entrainment of sediments into water flow:
qCRIT= 0.78 dM1.5 tanϑ-1.27 (2)
Equation (1) corresponds to a debris flow to be generated in a short distance, while equation (2) concerns the limit for the high rate sediment entrainment to have the generation of a debris flow. For these reasons, equation (1) provides values of qCRIT about four times larger than equation (2). Moreover, Gregoretti and Dalla Fontana (2008) compared the estimates of the critical discharge provided by equation (2) with the simulated values of runoff peak discharge of about 30 debris-flow events occurred on the Dolomites in the period 1993-2006. Figure 3 shows that equation (2) in its dimensionless form, represents an inferior limit for the simulated peak discharge of all the events. Recently, Pastorello et al. (2020) proposed a relationship analogous to those of Tognacca et al. (2000) and Gregoretti and Dalla Fontana (2008) for the critical discharge corresponding to the occurrence of high magnitude debris flows.

The peak value of the solid-liquid discharge is computed according to the relationship provided by Takahashi (1978, 2007) and updated by Lanzoni et al. (2017) on a base of systematic series of debris flows generated in a laboratory flume:
QP=0.75c*/(c*- cF ) QPL (3)
where QP is the peak solid-liquid discharge, c* is the dry bed sediment concentration, cF is the sediment concentration at the front of the debris flow and QPL is the peak runoff discharge. This relationship is based on the mass conservation equation and assuming the maximum value allowed for cF = 0.9 c* (Takahashi, 2007) the peak solid liquid discharge can grow up to 7.5 times of the peak runoff discharge. Field data shows that this amplification factor could be underestimated (Kean et al., 2016). In literature there are some relationships for the estimating cF (Gregoretti and Degetto, 2012). Here that of Takahashi (1978) updated by Lanzoni et al. (2017) is shown:
cF=tanϑ/((ρ_S/ρ-1)(tanϕqs-tanϑ)) (4)
where ϕqs is the quasi-static friction angle (ratio between shear and normal stresses in the region just over the static bed).
The solid-liquid volume,VSL, is computed combining the runoff volume contributing to debris flow, VL (blue dashed area in figure 1), with or the sediment volume VSED or the mean sediment concentration c. The sediment volume can be saturated and in this case:
VSL = VL+ VSED = VL + VS/c* (5)
otherwise:
VSL = VL + (1 – c*)SVS/c* (6)
where VS is the solid volume and S the saturation degree of the entrained sediments. Equations (5) and (6) can be written using the mean sediment concentration c (VS/VSL). Substituting VS with c VSL equations (5) and (6) becomes:
VSL = VL /(1 – c/c*) (7)
VSL = VL /(1 – (1-S)c -cS/c*) (8)
Known QP and VSL the solid-liquid hydrograph is determined because its duration is fixed: tI = 2 VSL/QP (figure 4).
The value of QP is determined after the computation of QPL and cF, known the characteristics of sediments (c*, ϕqs) and morphology (ϑ) in the initiation area. The value of VSL is estimated also by VS or c. These last values depend on the entrainment rate that increases with the peak runoff hydrograph and slope (Lanzoni et al. 2017) and on the length of the reach between the formation of the front and the reference location where the solid-liquid hydrograph should be estimated. In the case of Rovina di Cancia, the values of VSED and c can be estimated using data of previously occurred debris flows (simulated runoff hydrographs and sediment volume entrained and deposited during debris-flow routing). The analysis of data of the entrained volume of sediments on the reach between the altitude of 1666 m a.s.l. and the flat area at altitude of 1344 m a.s.l. (see the description of the site of Cancia) and the estimates of the runoff volume contributing to debris flow for the debris flows occurred on 18 July 2009, 23 July 2015, 4 August 2015, 1 July 2020 and 29 August 2020, provides an average value of c = 0.5 (0.38 < c < 0.56) after assuming S = 1 and c* = 0.62 (Gregoretti et al., 2019). This value is that to be used for the estimate of the sediments volume transported by the debris flow upstream the flat depositional area. The data of all the sediments volumes transported by the debris flows occurred on 1994-2020 show that it is 10000 m3 the value of the sediments volume retained by the flat deposition area and by the upstream reach.
THE webGIS PLATFORM
The INADEF-EWS is a web-based software solution that integrates meteorological and geomorphological data and models, and provides to the final user real-time information on debris-flow hazards for selected sites (watersheds).
INADEF-EWS is constantly fed with rainfall nowcasts generated by the INCA model, and uses these input data to run a runoff simulation model (ZEMOKOST) and in turn a triggering model and a model estimating discharge and volume. The triggering model outputs are finally used to identify actual debris flow-related hazards.
The INADEF-EWS has been developed using only open-source software platforms and solutions (e.g.: PostgreSQL/PostGIS, GeoServer, and OpenLayers).
INADEF-EWS uses a classical client/server architecture: the server (back end) is in charge of managing data input/outputs, running models, and serving data to the client. The HTML5 client in turn presents the data to the end users in the form of a responsive web page, that can therefore be accessed by any device connected to the world wide web.


